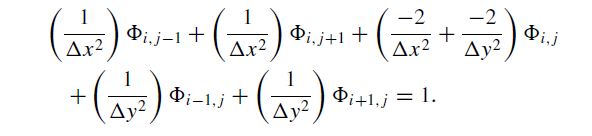thanks to Mr.Sungkono, Boss Asdi Presetyo, Boss Jordan Eko Setiyawan who have shared at whole night.
clear all;
clc;
L=zeros(1271,1271);
px=1000/30;
py=1500/40;
for i=43:1229
n=41;
L(i,i-1)=1/py;
L(i,i+1)=1/px;
L(i,i-n)=1/px;
L(i,i+n)=1/py;
end
for i=1:29
n=41;
L(i*n+1,:)=0;
L(i*n,:)=0;
end
for i=1:1271
L(i,i)=(-2/px)+(-2/py);
end
R=zeros(1271,1);
for i=43:1228
R(i,1)=1;
end
for i=1:29
n=41;
R(i*n+1)=0;
R(i*n)=0;
end
L
R
x=L\R
for i=1:1:41
for j=1:1:31
k = (j-1)*41+i;
phi(i,j) = x(k);
end
end
phi
% Making vectors for nodal points positions
x=1:31; % Horizontal
y=1:41; % Vertical
% Making new figure
figure(1);
% Plotting solution
surf(x,y,phi);
light;
shading interp;
colorbar;
lighting phong;
title('Solution of 2D Poisson equation')
xlabel('x, km')
ylabel('y, km')
zlabel('Gravity potential, J/kg')
I belive that what I write above have any lack. I sincerely receive any comment to make it better. thanks
Wednesday, 18 March 2015
Tuesday, 17 March 2015
solution 2D POISSON equation
Alhamdulillah...
I hope Allah SWT keep me from USELESS knowledge, keep me from VAIN activity, keep me from NO SOLEMN feeling, keep me from unsatisfied desire, and keep me from unanswered prayer. amin
then, I would like to give enormous thank to Mr Sungkono M.Si who forces me to study computation physics and always inspire me in using MATLAB.
now we try to get solution of 2D Poisson equation using finite differences and we will visualise the solution. the governing equation is given by
we use regular grid of 5 X 5 points and the model size 50 X 50 km. A finite-difference representation of the Poisson equation in 2D can be derived
then, we will get desain of node that we need to find the solution in a node. see this figure,
then the general solution
note: you have to change general solution value indices from geometrical indices(i and j) to global index of unknown k.
where Ny is vertical resolution.
L=zeros(25,25);
p=50/4;
q=50/4;
for k=1:5
L(k,k)=1;
end
for k=7:19
n=5;
L(k,k)=(-2/p)+(-2/q);
L(k,k-1)=1/q;
L(k,k+1)=1/p;
L(k,k-n)=1/p;
L(k,k+n)=1/q;
end
for k=21:25
L(k,k)=1;
end
for k=1:3
n=5;
L(k*n+1,:)=0;
L(k*n,:)=0;
end
for k=1:25
L(k,k)=(-2/p)+(-2/q);
end
R=zeros(25,1);
for k=7:19
R(k,1)=1;
end
for k=1:4
n=5;
R(k*n+1)=0;
R(k*n)=0;
end
L
R
x=L\R
for i=1:1:5
for j=1:1:5
k = (j-1)*5+i;
phi(i,j) = x(k);
end
end
phi
% Making vectors for nodal points positions
x=1:5; % Horizontal
y=1:5; % Vertical
% Making new figure
figure(1);
% Plotting solution
surf(x,y,phi);
light;
shading interp;
colorbar;
lighting phong;
title('Solution of 2D Poisson equation')
xlabel('x, km')
ylabel('y, km')
zlabel('Gravity potential, J/kg')
I hope Allah SWT keep me from USELESS knowledge, keep me from VAIN activity, keep me from NO SOLEMN feeling, keep me from unsatisfied desire, and keep me from unanswered prayer. amin
then, I would like to give enormous thank to Mr Sungkono M.Si who forces me to study computation physics and always inspire me in using MATLAB.
now we try to get solution of 2D Poisson equation using finite differences and we will visualise the solution. the governing equation is given by
we use regular grid of 5 X 5 points and the model size 50 X 50 km. A finite-difference representation of the Poisson equation in 2D can be derived
then, we will get desain of node that we need to find the solution in a node. see this figure,
then the general solution
note: you have to change general solution value indices from geometrical indices(i and j) to global index of unknown k.
where Ny is vertical resolution.
L=zeros(25,25);
p=50/4;
q=50/4;
for k=1:5
L(k,k)=1;
end
for k=7:19
n=5;
L(k,k)=(-2/p)+(-2/q);
L(k,k-1)=1/q;
L(k,k+1)=1/p;
L(k,k-n)=1/p;
L(k,k+n)=1/q;
end
for k=21:25
L(k,k)=1;
end
for k=1:3
n=5;
L(k*n+1,:)=0;
L(k*n,:)=0;
end
for k=1:25
L(k,k)=(-2/p)+(-2/q);
end
R=zeros(25,1);
for k=7:19
R(k,1)=1;
end
for k=1:4
n=5;
R(k*n+1)=0;
R(k*n)=0;
end
L
R
x=L\R
for i=1:1:5
for j=1:1:5
k = (j-1)*5+i;
phi(i,j) = x(k);
end
end
phi
% Making vectors for nodal points positions
x=1:5; % Horizontal
y=1:5; % Vertical
% Making new figure
figure(1);
% Plotting solution
surf(x,y,phi);
light;
shading interp;
colorbar;
lighting phong;
title('Solution of 2D Poisson equation')
xlabel('x, km')
ylabel('y, km')
zlabel('Gravity potential, J/kg')
Subscribe to:
Comments (Atom)